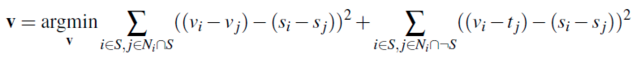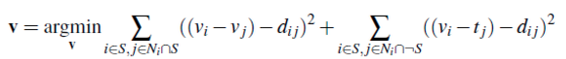Project 2: Gradient-Domain Fusion
In this project, we blended a region of interest (ROI) in one image onto another image using Poisson blending and gradient mixing. For both these techniques, we solve our output image by using a least squares approach.
Toy Problem - Image reconstruction using image gradients
In the algorithms used in this assignment, we solve for an output image using a least squares approximation. This approach is used to solve overdetermined systems by minimizing an error function (also see linear regression). Interestingly, least squares approximation can be used in processing images. For this assignment, we will use it for image blending.
But first... we must gain a better understanding of image reconstruction using least squares approach. We want to minimize the error in an overdetermined system (i.e. minimize ||(Ax -b) ||, where x is the output image pixels listed in a column, A is an MxN matrix that describes the weight of each output pixel (a total of N pixels depending on the dimension of the image) in a system of M equations, and b is a column of M solutions for the M equations. We can list many equations for producing a desired output image. For example, what would happen if A were an identity matrix? Then the output image pixels would simply be the same as the values listed in the vector b.
In this part of the assignment, we reconstructed an image based on its gradient. In other words, we wanted to solve the least squares problem such that the gradient of the output image matched the gradient of the input image. Shown here is a grayscale image, its x-gradient, and its y gradient.
Toy Problem - Image reconstruction using image gradients
In the algorithms used in this assignment, we solve for an output image using a least squares approximation. This approach is used to solve overdetermined systems by minimizing an error function (also see linear regression). Interestingly, least squares approximation can be used in processing images. For this assignment, we will use it for image blending.
But first... we must gain a better understanding of image reconstruction using least squares approach. We want to minimize the error in an overdetermined system (i.e. minimize ||(Ax -b) ||, where x is the output image pixels listed in a column, A is an MxN matrix that describes the weight of each output pixel (a total of N pixels depending on the dimension of the image) in a system of M equations, and b is a column of M solutions for the M equations. We can list many equations for producing a desired output image. For example, what would happen if A were an identity matrix? Then the output image pixels would simply be the same as the values listed in the vector b.
In this part of the assignment, we reconstructed an image based on its gradient. In other words, we wanted to solve the least squares problem such that the gradient of the output image matched the gradient of the input image. Shown here is a grayscale image, its x-gradient, and its y gradient.
First I create an A matrix that "took" the y-gradient of an image. To check if it worked, I multiplied the A matrix by the original image in column format. Shown is a small portion of the A matrix (100x100) that takes the y-gradient. Also shown is the image that results after multiplying this matrix by the original image. As you can see, the matrix multiplication computes an image that is the same as the Y gradient shown above. Note that the output array b must be reshaped to form a 2D image.
I did the same for the x-gradient. A portion of the A matrix that computes the x-gradient is shown (400x400). I again tested it by multiplying the A matrix by the original image in column form. The resulting image is the x-gradient of the original image so I know that it is working.
To actual solve for x in this equation, we need to set b to equal something. Because these A matrices take the gradient of the image, then the b matrix must contain the gradient of the image we want to reconstruct when solving for x. In other words, we want to solve the following least squares problem:
1. minimize (v(x+1,y)-v(x,y) - (s(x+1,y)-s(x,y)))^2
2. minimize (v(x,y+1)-v(x,y) - (s(x,y+1)-s(x,y)))^2
where s is the source image and v is the output image. Now the A matrix is the combination of the two matrices above stacked on top of each other, and b is the y-gradient and x-gradient of the original image in a big column. There is an additional constraint added so that the intensity values match the original image:
3. minimize (v(1,1)-s(1,1))^2
Here is the result.
The reconstruction looks really good. Shown below is an example of an earlier failed reconstruction when I first started the homework. The error was due to incorrectly placing the 1's in the x-gradient portion of the A matrix.
Poisson Blending
Now we move onto the second part of the assignment on Poisson blending. We want to take a source region S from a source image called s, and blend it onto a target image t. There are several steps to this process.
1. Select a source and target image
2. Select the region of interest (ROI) in the source image
3. Align the ROI in the target image
4. Construct an A matrix that has the following constraints:
a. If the pixel is not in the ROI, then the output pixel should have the same value as the target image
b. If the pixel is in the ROI and none of its 4-neighbors is on the border of the ROI, then the gradient of the 4-neighbor
pixels of the output pixel should match the 4-neighbor gradient of the source image
c. For a pixel in the ROI in that has a 4-neighbor on the border of the ROI, the gradient between that pixel and that
neighbor should match the gradient of target image.
This is stated more clearly and concisely with math listed in the homework:
Now we move onto the second part of the assignment on Poisson blending. We want to take a source region S from a source image called s, and blend it onto a target image t. There are several steps to this process.
1. Select a source and target image
2. Select the region of interest (ROI) in the source image
3. Align the ROI in the target image
4. Construct an A matrix that has the following constraints:
a. If the pixel is not in the ROI, then the output pixel should have the same value as the target image
b. If the pixel is in the ROI and none of its 4-neighbors is on the border of the ROI, then the gradient of the 4-neighbor
pixels of the output pixel should match the 4-neighbor gradient of the source image
c. For a pixel in the ROI in that has a 4-neighbor on the border of the ROI, the gradient between that pixel and that
neighbor should match the gradient of target image.
This is stated more clearly and concisely with math listed in the homework:
The ROI and corresponding mask was selected by using the function supplied called, "getMask.m" After the ROI is created, the images are aligned using another function supplied called, "alignSource.m" The biggest challenge in this alignment stage is resizing the images so that the ROI is the appropriate size on the target image. Also you don't want the images to be too high resolution or you will be waiting for too long and going crazy and impatient.
To start I am showing the sample images provided of the baby penguin and people walking on a snowy mountain. Just a sanity check, because I knew that this example had to work.
To start I am showing the sample images provided of the baby penguin and people walking on a snowy mountain. Just a sanity check, because I knew that this example had to work.
As you can see, the penguin is not blended well onto the target image before using Poisson blending. I constructed an A matrix based on the arguments that needed to be minimized (listed above). The technique of creating an A matrix is similar to part 1 of the assignment. Here is the output image after solving for b and reshaping:
|
It works! I have a few other examples that I will show now. When using this algorithm, there were a few important things to consider for achieving the best results:
|
My final example is one to demonstrate when Poisson blending doesn't work so well. There is Europa, and I want to blend it into the daytime sky. Unfortunately the source image of Europa has the dark void of space in the background. Therefore, it does not blend well with the target image. As a result, Europa loses its color and we see only the details in white over the daytime sky in the target image.
Gradient Mixing
Now for the final part of the assignment, which is very similar to part 2. We again want to blend an ROI from one picture onto another picture, but this time we want to keep better track of the target image gradient in the ROI. Steps 1-3 listed in part 2 are the same, but the least square arguments are slightly different.
In the ROI, we calculate the 4-neighbor gradient in the source image as well as the 4-neighbor gradient in the target image. Whichever gradient that has the highest magnitude is then stored in the b array. In other words, we want the the gradient of an output pixel to match which ever gradient is larger between the target and source image at that pixel.
This is stated more clearly and concisely with math listed in the homework:
Now for the final part of the assignment, which is very similar to part 2. We again want to blend an ROI from one picture onto another picture, but this time we want to keep better track of the target image gradient in the ROI. Steps 1-3 listed in part 2 are the same, but the least square arguments are slightly different.
In the ROI, we calculate the 4-neighbor gradient in the source image as well as the 4-neighbor gradient in the target image. Whichever gradient that has the highest magnitude is then stored in the b array. In other words, we want the the gradient of an output pixel to match which ever gradient is larger between the target and source image at that pixel.
This is stated more clearly and concisely with math listed in the homework:
where dij is which ever image gradient is larger at that pixel and neighbor. This approach works well when writing is being placed on a detailed background. Here is an example.
And now here are some close ups of the ROI after Poisson blending and gradient mixing. You can see that which blending technique produces the best results depends on the situation. Sometimes it is difficult to see a difference
|
Aligned before blending
|
Poisson blending
|
Gradient mixing
|